900. Кирпичная стена

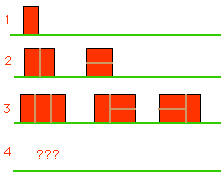
Из кирпичей размером 1 * 2 следует построить стену длины n и высоты 2. Сколькими способами это можно сделать?

Вход. Каждая строка содержит длину стены n (n £ 50). Последняя строка содержит n = 0 и не обрабатывается.

Выход. Для каждого входного значения n вывести количество способов, которыми можно построить кирпичную стену размером 2 * n .

Пример входа

1

2

3

0

Пример выхода

1

2

3

РЕШЕНИЕ

числа Фибоначчи

Анализ алгоритма

Обозначим через f(n) количество способов, которыми можно построить кирпичную стену высоты 2 и длины n. Тогда можно положить один кирпич вертикально и далее строить стену длины n – 1 f(n – 1) способом, или положить два кирпича горизонтально и строить стену длины n – 2 f(n – 2) способами. То есть f(n) = f(n – 1) + f(n – 2). Также имеем: f(1) = 1 (один вертикальный кирпич), f(2) = 2 (два вертикальных или два горизонтальных кирпича). То есть f(n) является (n + 1) - ым числом Фибоначчи.

Реализация алгоритма

Поскольку n £ 50, а 51 – ое число Фибоначчи выходит за пределы типа int, то следует воспользоваться 64 битовым целочисленным типом long long.

#define i64 long long

i64 fib[51];

В массиве fib[51] сгенерируем все числа Фибоначчи согласно выше приведенным начальным условиям (fib[i] = F_i+1).

fib[1] = 1; fib[2] = 2;

for(i=3;i<51;i++) fib[i] = fib[i-1] + fib[i-2];

Для каждого входного значения n выводим соответствующее ему число Фибоначчи.

while(scanf("%d",&n),n)

printf("%lld\n",fib[n]);